
Games are a growing trend in crypto, with many games trying to be as "onchain" as possible in order to maximize composability. However, building onchain games can often lead to increased latency in the game as transactions need to settle to the underlying chain.
There are many directions projects are innovating in to try and reduce the latency while maintaining composability, with ZK cryptography being one of the most promising. In this paradigm, the goal is to enable players to play local-first, and then only synchronize with the chain as little as needed with a ZK proof of the actions they took.
An example of why this would be useful is our game Tarochi, whose battle system involves turn-based combat with a stamina bar (seen in yellow in the screenshot below)
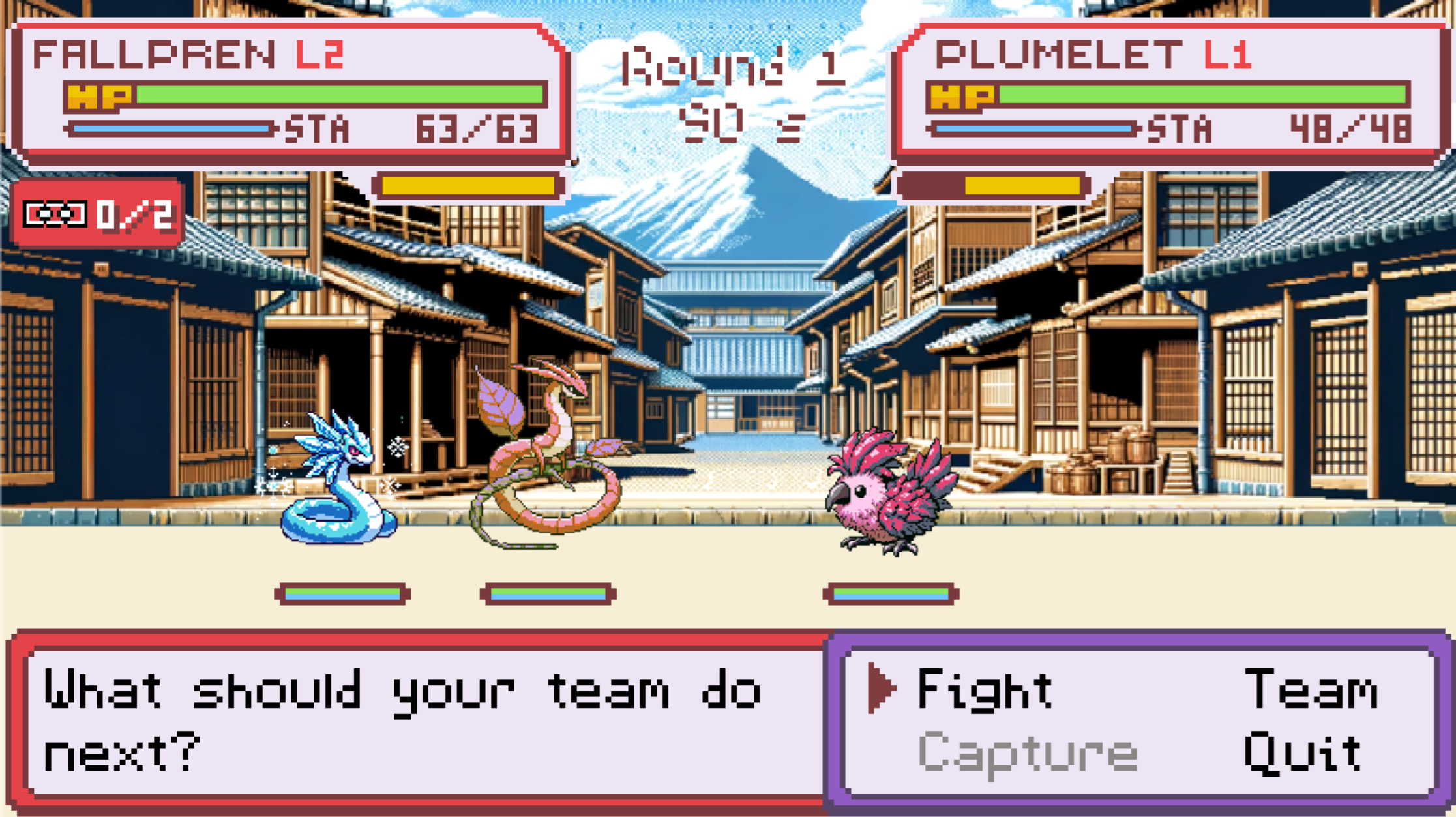
Ideally, the battle system in Tarochi would happen within a ZK environment: the entire battle happens locally first, and then you submit the result of the battle onchain as a ZK proof.
However, how can we power the stamina bar (which restores during the battle based on the passage of time)? Typically, implementations use the block time of the underlying chain, but if the game is running locally there is no clock that we can reference.
One option is leveraging the clock of the underlying chain, but this requires to settle to the chain which, if the block time of the underlying chain is 2s, could introduce up to 2s of latency for the player's move to be submitted.

More generally, this problem affects anything that requires timers, from stamina bars, to cooldowns and more.
One way we could solve this is if we had a cryptographic technique (something that depends entirely on cryptography and not trusting the user's clock which can easily be modified by the user) that can approximate a duration of time.
If we have such a technique, we could use it to not only solve this problem, but it can even be extended to proving the passage of a large amount of time (ex: 1hr) by using recursive SNARKs to combine multiple proofs of the passage of a small amount of time into succinct proofs of a larger amount of time having passed. This is an important property, because battles in Tarochi can last multiple minutes, and so we need to interweave proofs of passage of time with user actions (ex: attacking the enemy) and merge them into a single final proof.
Fortunately, there is a technique called VDFs that can help us solve this problem.
What are VDFs?
VDFs are Verifiable Delay Functions: a family of functions which are slow to compute, but fast to verify. They come with some difficulty parameter that can be tuned to make function evaluation slower when needed to approximately match some target duration. These were introduced in BBBF18. Note that, conceptually, this is similar to Proof of Work (PoW) with some extra desirable properties.
Additionally, VDFs must have a unique output. This is because VDFs are designed to be used in encryption and randomness beacon, but if multiple outputs exist, then an adversary could bias the randomness in their favor or fake the message that was encrypted.
Notably, beyond efficient verification, they have the additional property that parallelization should not give a large advantage.
The goal of this is that even if you have multiple computers (or even a single computer with multiple cores), you do not gain a large advantage over other users. The reason this is a useful properly is because although CPUs continue to get faster, individual core clock speeds have stopped growing as fast which puts and different users on a fairer playing field
Similarly, ASICs ideally do not give a large advantage either, otherwise the power users can dominate the game with specialized hardware (although there is less of an incentive to run ASICs for a game compared to financial use-cases)
VDF vs related techniques
Iterated hashing
One tempting way to implement a VDF is to use iterated hashing. For example, use a common hash function like sha256 in the following way:
result = sha256(initial_seed) # 1st iteration starts with some known seed (ex: block hash start calculating
result = sha256(result) # iteration 2
result = sha256(result) # iteration 3
...
The problem with this approach is that it's not quite a VDF. Notably, there is no way to efficiently verify the result (if somebody give you the starting seed, the result, and tells you they computed 100 iterations of sha256, you will have to compute 100 iterations yourself to verify the result matches).
In fact, Solana uses this kind of iterated SHA256 for their Proof of History (PoH), where all block producing nodes in the network have to calculate their own version of the VDF locally based on the transactions in the network and the passage of time.
Turning iterated hashing into a VDF
Can be made VDF-like through recursive SNARKs. Notably, if you compute sha256 100 times inside a recursive SNARK, you can have a succinct proof of the result which can be verified quickly.
Using a similar idea, you can turn almost any computation that takes a long time into a VDF using recursive SNARKs thanks to the fact that it makes verification efficient. However, it doesn't mean it's a good VDF. Notably, it increase the attack vector of your VDF quite significantly in two ways:
- Recursive SNARK calculations often has some points of parallelization (it would be hard, and probably undesirable, to create a special ZK SNARK technique that cannot be parallelized)
- Recursive SNARKs, due to the their complexity, can vary in their performance a lot depending on the user's hardware. In fact, there is a high economic value in creating ASICs for common constructions as they can be used to operate prover networks or nodes for blockchain networks based on these techniques.
This idea was originally discussed in the original VDF BBBF18 paper
ZK-friendly iterated function
When thinking about the ZK setting, the properties of a good function to iterate with changes slightly. Notably, we want a function that has a high prover time while being encoded in as few gates as possible to keep the verifier time small.
This makes a big difference. For example, the verification complexity of Sloth++ (which tries to use a ZK-friendly function) has a 7000-fold improvement over iterated sha256. In a future section, we'll talk more about MinRoot, which (at the time of writing) is the state of the art in this direction.
Timelock puzzles (TLPs)
TLPs are a cryptographic technique to try and make information only available at a future time. The goal is that creating the puzzle is easy, but solving the puzzle is hard. Notably, the paper that defined these is RWA96 which defines the RWA assumption: given a group element x and an integer T with an RSA group N, it's hard to compute x^(2^t) mod N in parallel time (the best approach being to calculate it sequentially yourself and checking the result).
VDFs are based on this idea, as you could encrypt a message where the decryption key is the result of computing a VDF (so that anybody that wants to decrypt it has to calculate the VDF themselves to retrieve the decryption information)
Proofs of Sequential Work (PoSW)
Proofs of Sequential Work are similar to VDFs, but with two key properties dropped:
- The verification doesn't need to be efficient (it can be an iterated hash function)
- The output does not need to be unique
These were introduced by MMV13, and then improved in CP18 so that they only require logarithmic space
Open question: although utilizing VDFs as a source for randomness for games is great, the same thing can be achieved by introducing a VRF. Does dropping the uniqueness requirement give us any benefits in the ZK setting?
Timelock encryption
Unlike timelock puzzles, timelock encryption encrypts data at a future date that requires no computation to do the unlock. Instead, the information required to reveal the information is generated by a decentralized network (where as long as a majority of the network is honest, nobody can decrypt the information ahead of time)
You can learn more about this technique in a video by our team here
Classical VDFs
There are two VDFs implementations based on the RSW assumption typically referenced that both have a Rust implementation:
Classical VDFs have a great property: they don't rely on ZK. This means we can run the prover in a non-ZK setting (lowering the surface area that can be sped up with beefy hardware) and only have to run the verifier in a ZK setting if we want to be able to combine proofs together.
However, both of these come with their own challenges even just to operate the verifier in a ZK setting. The common problems are:
- Both operate using RSA which requires at least 2048-bit numbers for security, making them computationally expensive in a ZK setting as these numbers exceed the field size of elliptic-curve based recursive SNARK systems.
- Both rely on groups of unknown order (GUOs). The simplest such group is the RSA group, but it requires a trusted setup (the order N needs to be the product of two unknown primes). An alternative without a trusted setup is to use class groups of an imaginary quadratic field (often shorted to just "class groups")
Using the RSA group
Implementations of Wesolowski & Pietrzak often use class groups of an imaginary quadratic field using the binary quadratic form instead of the RSA group to avoid the need for a trusted setup.
However, multiplication when using the binary quadratic form requires computing greatest common divisor (gcd) calls on large numbers which has proven to be prohibitively slow in our benchmarks even for non-extended euclidean gcd for a single gcd call (where many such GCD calls would be required to verify a VDF)
On our benchmarks, computing the following GCD using o1js takes ~1hr
gcd(
66192067702349471902822889917521630986608145681764058902797324107655626550548394747593124784626505148515147440884312503123977915307410797250481114283716893992887254383889295241096466408449603762914352825104572615207366531086433177129596279528363570312063132413328722950462592090559000063264135584309478448349n,
64994285377340214206572207534835868053851007183284265013844951369449810556767127886232672704240625827623339904466957865609336308250664600055526550318867746860900055215309858041282435305032854457866704943529828131858657354140245647370594766415054469927382930751337852515318596998217230438351735326293886615645n
)
open question: given this, is an RSA group version of VDF implementations over class groups faster?
Wesolowski
Wesolowski has a single-round protocol (constant sized proof!) of repeated squares. However, its fiat-shamir transformation for making it non-interactive requires hashing a set of parameters to a large prime number in the group (the reason you need a prime is to avoid an attack outlined in section 3.2 of BBF18)
Finding such a prime deterministically is already hard to obtain in the classical setting on large numbers. Currently implementations do this by using the hash of the parameters as a starting point, and then iteratively running primality tests on an increasing number until one number is found to be probably prime with sufficiently low error rate. Doing this in the ZK setting is computationally expensive as you need to run many primality tests iteractively which may require a very large amount of iterations
More concretely, although there are many primality tests, the one commonly used in Wesolowski implementations is Miller-Rabin, which requires multiple iterations, each consisting of exponentiation (not cheap).
We also know that, in the native implementation, we have to run the primality test for many candidate numbers given that the prime number theorem states that the gap between a prime number p and the next prime number tends to ln(p). If our hash is unlucky and we guess (p+1), the next prime is approximately ln(p)-1 numbers away. If we use a 256-bit hash function, that number can be ln(2^256 - 1) = 177 numbers away.
A more ZK-friendly primality test
There are three kinds of primality tests:
- Monte Carlo probabilistic tests: tests that may give false positive
- Las Vegas probabilistic tests: test that may give false negatives
- Deterministic algorithms: algorithms that determine the primality without chance of error
Although in a classical setting Monte Carlo algorithms like Miller-Rabin have better performance, in a ZK setting, Las Vegas tests work well because we can find the right parameter in a non-ZK setting, and then run the test on the single input required in a ZK environment. Deterministic algorithms also work, but are often prohibitively computationally expensive.
This means you have to choose the primality tests carefully.
Open question: what is the performance of all the common primality tests in a ZK setting?
Better Monte Carlo primality tests
If using a Monte Carlo test such as Miller-Rabin, in the negative case (where a number is not prime), the ZK proof is simpler: you can find which primality test fails in which condition for the number, and provide that as an input to the prover so it can quickly rule out non-primes. Unfortunately, this still has two problems:
- The proof may still take some time to generate. For example in the case of Miller-Rabin, even if you know the
avalue where the primality test fails, checking that it fails can still be expensive. - Even if you manage to rule out primes efficiently, you still run into an issue that in the "probably prime" case, you really do have to run the full test, which can be the main performance bottleneck (fortunately for Miller-Rabin, the larger the number the fewer iterations you have to do)
Proof by construction using Las Vegas primality tests
Many primality tests are recursive in nature, in that they rely on the knowledge of the existence of some smaller prime. One such test is the Pocklington which is a Las Vegas probabilistic test.
The benefit of these recursive primality tests is that they can be used to form primality certificates: a set of information that can be used to check the primality of a number. Pocklington is particularly useful here, because every prime can be represented with a Pocklington primality certificate (which we can use to avoid losing entropy in our fiat-shamir transformation)
We cannot start by hashing to a large value (say, 2k-bits), and then finding the first prime with Pocklington, otherwise we are stuck in the same problem as the Monte Carlo case where we have to reject possible hundreds of non-prime numbers. Instead, we try to construct a prime as close as possible to the target length 2k-bits using 2k-bits of entropy.
Fortunately, there exists an implementation of such an algorithm is outlined in OWWB19 with corresponding Rust code. Using their notation for the Pocklington's Criterion, it works by:
- Use 32-bits of entropy to hash to a 32-bit prime using the Monte Carlo primality test approach (relatively fast given we're working with smaller numbers, and gives us our initial random starting point)
- While we still have entropy remaining,
- Supposed we have a prime
pcurrently at entropye_p - Generate a random number
xconsumingmin(entropy_remaining, e_p)entropy - Find some value
a(you can check iteratively check every value from2, ..., infinity) that satisfies Pocklington's Criteria - Set
N(N = xp+1) to be the next prime numberp
- Supposed we have a prime
- Although the prover gets to choose the value of
afor the primality certificate,- There is enough entropy in the calculation that it doesn't allow them to meaningfully bias the algorithm in their favor
- The value of
ais provided to the verifier as part of the primality certificate, so the verifier doesn't have to regenerate it
Note that:
- This algorithm maps to nearly possible prime numbers (the smallest primes are left out, as the value is always increasing every loop iteration), so this gives us near the minimum size prime number range we could get for this much entropy (there are other Pocklington-based techniques we could use to get a large prime number faster, but they use less entropy to get there which we want to avoid).
- Every step we double the entropy. In practice, the OWWB19 construction is slightly less than 2x per step, and so it creates 256-bits of entropy in 5 steps (generating a 322-bit prime number)
open question: the reference implementation of OWWB19 has some TODOs to try and maybe get a few extra bits of entropy, so the details of this algorithm may be very slightly improved. More generally, there could exist a more optimal construction (although it could be that a better fiat-shamir transformation gets us down to only requiring k bits instead of 2k, which could be a more impactful research direction)
open question: what is the actual cost of implementing the OWWB19 technique in o1js?
open question: is there a variant of the Pocklington's Criteria based on elliptic-curve primality proving? Maybe such an approach is faster for pairing-based crypto. You can see more about how to implement a hash of entropy into a point in a prime-order subgroup in WB19
open question: the OWWB19 paper targets 256-bits of entropy. Do we need that much? Numbers of 322-bits are slightly over the max field size of Mina, which incurs a performance hit. The reason for the choice of using 2k bits is described in section 3.3 of BBF18
open question: is there a way to re-use some of this work between VDF iterations to reduce the overhead? Section 7 of Wes19 talks about aggregation, but it's unclear if this construction increases the entropy proportional to the number of inputs you aggregate (if that's the case, probably keeping entropy small and aggregating via ZK is faster than computing on larger entropy numbers)
Other technique
Open question: is there a different way to apply fiat-shamir to Wesolowski that is more ZK-friendly than the two mentioned? There have been two papers in this direction: SBK24, which was then improved on by CLR24 which (at the time of writing) is in the process of being implemented in Rust here. It remains to be seen how well this direction performs in a ZK setting, but its performance in a classical setting is promising.
Pietrzak
Pietrzak does not require picking this kind of random prime, making it easy to ZK verify. Pietrzak's VDF also has the ability to shift more work to the prover as needed away from the verifier (in exchange for increasing the circuit size) which it calls a delta parameter. This delta should be set to maximally do work in the prover to minimize the circuit size in the verifier
TODO: is there any reference implementation of Pietrzak using RSA groups? One exists comparing RSA vs class groups of an imaginary quadratic field for Wesolowski here. Maybe this can be used?
TODO: Does Pietrzak require p,q to be safe primes for RSA groups? The paper BBF18 mentions in section 6 that this isn't required as long as you use a transformation on the RSA group to avoid violating the low-order assumption. This post here by seems to have the same conclusion that it should be safe to omit this property.
Open question: is there any way to write custom gates/precompiles for a ZK system that could speed up computation?
Open question: is there any publicly known value for N for an RSA group that is known to have this safe prime property? BBF18 mentions in section 6 that using safe primes isn't required as long as you use a transformation on the RSA group to avoid violating the low-order assumption, but if one exists, we might as well use it if we know it's honestly generated
Open question: is there any publicly known value for N for an RSA group that was generated via a ceremony we can reuse? (even if it doesn't have the safe prime property). Ethereum attempted one, but an audit by ZenGo revealed some errors in the implementation and the project was abandoned before any value for N was generated.
Other approaches
Open question: are there other techniques where the computation is expensive, whose verifier is also expensive (but not quite as expensive as the initial computation) but can be made cheap through wrapping in a ZK proof? This may seem like a strange set of requirements, but it may be an unexplored area in VDF construction.
Open question: is it better to batch VDF verification together instead of doing it incrementally? There is some literature talking about batched VDF verification. This can help reduce the overhead with spinning up an environment to generate a ZK proof
Open question: groups of unknown order are not quantum secure. It is an open question if any good quantum-resistant VDF exists
Open question: for games, we typically want a continuous computation as the clock for the game is always running. Does this allow for any optimizations?
Open question: Is using an elliptic-curve variant of RSA faster? See KMOV91, Dem94. You can see more about how to implement a hash of entropy into a point in a prime-order subgroup in WB19 if we use Wes19 which requires a hash-to-prime implementation.
Open question: are there ideas that can be taken from the DARK paper, which uses groups of unknown order like the RSA group to construct ZK circuits with quasi-linear proving time, but logarithmic verification time?
Continuous VDFs
There is a concept called a continuous VDF (cVDF) introduced in EFKP20 that allows you to set a large time parameter for your VDF (ex: 1hr computation), but optionally decide to prove an intermediate state (ex: 20 minutes) if needed.
The paper works by increasing the work done by the prover in a standard Pietrzak VDF to include more intermediate states. These intermediate states can be used as inputs to VDF verifiers to verify that part of the work has been completed.
This concept can introduce an important performance benefit for the gaming use-case: instead of setting a very fast clock time for the game (ex: 1s VDF proofs) which requires a lot of computation to aggregate with ZK, we can instead set a longer time period (ex: 1hr) so that little ZK work is in the case the user performs no action in the game, while still allowing the user to stop a VDF computation to perform an in-game action if needed (instead of having to compute until the full hour passes)
The comes at a cost by making that the proof generation itself is slower (the more granularity you want in the user's ability to stop a computation partway through, the larger the cost of the verifier). This means that this concept relies on having a sufficiently efficient ZK-Pietrzak VDF to work, and is not well suited for games with frequent actions.
Open question: when it this approach better? i.e. how many base clock intervals should the user skip (not submit any inputs) before this technique out-performs? (i.e. compare a VDF of base clock 1s vs a cVDF that can be abandoned every second as part of a larger clock time, and see how many seconds have to pass before the cVDF proof is cheaper to verify)
MinRoot
MinRoot is a candidate VDF by the Ethereum Foundation introduced in KMT22. It is based on the idea of ZKified iterative hashing with a more ZK-friendly function
Additionally, MinRoot has an existing implementation using Nova, as well as an ASIC implementation over pasta curves to empirically quantify the benefit ASICs get over average hardware.
Although it was decided that MinRoot will not be implemented in Ethereum do to concerns about its security against parallelism, this is given their strict requirement in a financial setting.
The work on MinRoot does not mitigate the fact that ASICs can be developed for scheme used to write the ZK circuit (or the fact these circuits can have a large performance difference between consumer computers).
Isogenies-based VDF
Iosgenies-based VDFs depend on the difficulty of random walks on an isogenie of elliptic curves, introduced in FMPS19
Open question: does the elliptic-curve nature of this construction give it better performance in a ZK setting?
Open question: is there any implementation of isognies-based VDFs that can be used in production? If not, why not?
- The answer seems it might be related to the size of the proof. The length of the random walk needs to be very large (ex: 7 * 10^(10) for a 1hr delay), and therefore storing each isogeny step for the proof can require terabytes of storage.
Open question: isogenies-based VDFs have a long setup. Does this negatively affects its usability for gaming use-cases?
Watermarking
To avoid the same VDF being reused, we need to encode:
- Information about the previous VDF iteration (or some information like the block hash if it's the first VDF the user is running)
- Information about the user's wallet (so it can't be reused among multiple players)
Open question: what is the best way to do this? The Wes19 paper talks about an approach for this, but we can probably do something better leveraging the fact that ZK proofs are privacy-preserving. Notably, for Wes19's construction, we can include the user's private key in proof so they can't easily outsource the proof without outsourcing their private key as well (or more weakly, include the user address in the entropy. This makes the proof easier to outsource without revealing your key)